1- Définitions

1.1 Les graphes

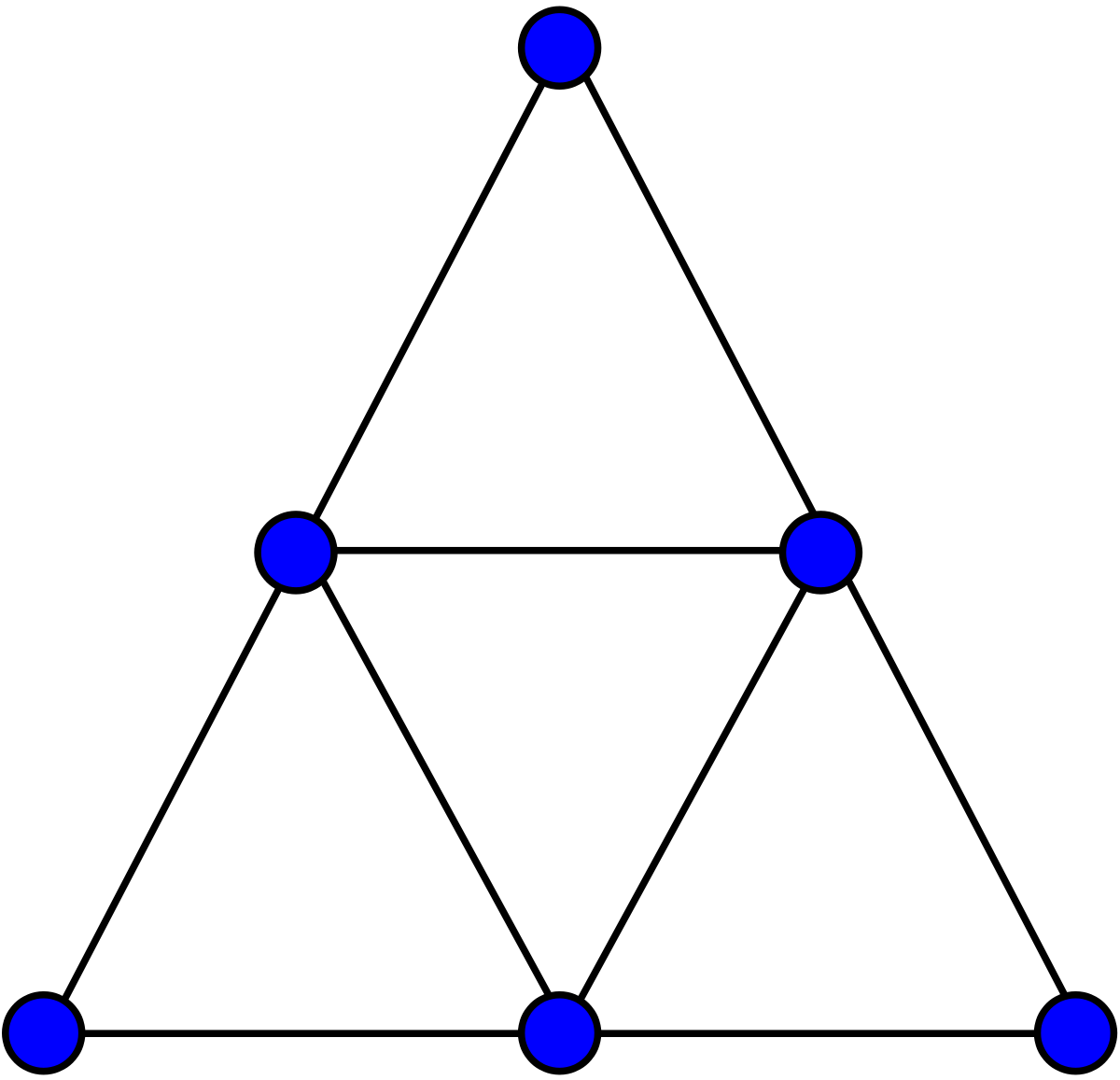
Nous appellons "graphe" un ensemble de points reliés par des arêtes. La structure de graphe est importante et intervient régulièrement dans de nombreuses branches des mathématiques et de l'informatique. Notons que le graphe peut se situer dans le plan, mais pas seulement. Nous pouvons également considérer des structures "graphiques" dans l'espace. Ici, tout ce qui nous intéressera concernant le graphe sera quelles arêtes sont attachées à quels points. Nous noterons \(\alpha\) le nombre de points total dans un graphe et nous noterons \(\beta\) son nombre d'arêtes. Nous noterons également \(a_0\) le nombre de points dans le graphe considéré qui n'ont pas d'arêtes (des points isolés), \(a_1\) le nombre de points qui ont une seule arête, \(a_2\) le nombre de points qui ont deux arêtes, etc. Nous considérerons toujours des graphes finis, où un point ne peut supporter qu'un nombre d'arêtes maximal \(p\). Ainsi nous auront toujours, dans n'importe quel graphe : $$\alpha = \sum_{i=0}^p a_i $$ Représentation d'un graphe (ici le graphe de Hajos) :

1.2 Les multigraphes

Pour les graphes simples, deux points ne peuvent être reliés que par \(0\) ou \(1\) arête mais jamais plus. Mais on peut considérer qu'il existe plusieurs chemins reliant ces deux points, et donc considérer que plusieurs arêtes puissent relier les deux mêmes points, c'est le concept du multigraphe. Il étend la notion de graphe au fait que deux points peuvent être reliés par plus que une seule arête.

1.3 Les hypergraphes

Le concept d'hypergraphe généralise encore celui de graphe. Pour un graphe, une seule arête ne pouvait relier que deux points (ou un seul si on considérait la notion de boucle), elle symbolisait un unique chemin. Mais on peut également imaginer qu'une arête puisse relier plus de deux points (qu'il y est des intersections menant à plusieurs arêtes). Ainsi le concept d'hypergraphe généralise celui de graphe dans le sens où dans un hypergraphe nous pouvons trouver tout type d'arêtes. Des arêtes reliant deux points (comme dans les graphes standards), mais également des arêtes reliant \(3\) points etc. Dans la suite et pour bien distinguer, nous noterons \(\beta_j\) le nombre d'arêtes dans le graphe reliant \(n_j\) points. Pour être plus clair, nous parlerons de "type d'arêtes". Le type d'une arête peut être entièrement défini par le nombre de points qu'elle relie ( \(n_j\)).

Dans toute la suite, nous travaillerons dans des "HM-graphes" des hyper-multi-graphe, dans le sens où ces graphes pourront contenir plusieurs types d'arêtes à la manière des hypergraphes, et plusieurs arêtes du même type pourront relier deux mêmes points à la manière des multigraphes.

2- Equations des HM-graphes

2.1 L'équation additive des HM-graphes

L'objet de l'équation additive des HM-graphes est : étant donné un HM-graphe, ayant \(\alpha\) points, \(\beta_1\) boucles, \(\beta_2\) arêtes reliant deux points, etc. comment formuler une équation reliant \(\alpha\) et les \(\beta_j\) ?

Nous allons tout d'abord exprimer le nombre d'arêtes \(\beta_j\). En reprenant les notations vues au dessus concernant les \(a_i\), nous noterons plus précisément \(a_{i,j}\) le nombre de points ayant \(i\) arêtes de type \(j\) (reliant \(n_j\) points). Et nous noterons \(p_j\) le nombre d'arêtes maximal de type \(j\) que peut supporter un seul point dans le HM-graphe. Ainsi nous avons toujours la relation pour un type d'arêtes donné : $$\alpha = \sum_{i=0}^{p_j} a_{i,j} $$

D'autre part, le fait qu'un point ait \(i\) arêtes de type \(j\) signifie qu'il existe \(i\) arêtes. Ainsi en multipliant le nombre de points ayant \(i\) arêtes par \(i\) nous obtenons le nombre d'arêtes total. Cependant avec ce raisonnement, comme une arête de type \(j\) est commune à \(n_j\) points, on comptera évidemment \(n_j\) fois le nombre d'arêtes. D'où la relation : $$ \beta_j n_j = \sum_{i=0}^{p_j} a_{i,j} i $$ Et donc : $$ \beta_j = \frac{1}{n_j} \sum_{i=0}^{p_j} a_{i,j} i$$

A partir de ces deux relations nous allons établir une équation reliant \(\alpha\) et les \(\beta_j\). En effet, il est alors assez simple de constater que si nous avons un HM-graphe avec \(m\) type d'arêtes alors : $$ m \alpha = \sum_{j=0}^m \sum_{i=0}^{p_j} a_{i,j}$$ $$ m \alpha = \sum_{j=0}^m \sum_{i=0}^{p_j} a_{i,j} (-i + i + 1)$$ $$ m \alpha = \sum_{j=0}^m \left( \sum_{i=0}^{p_j} a_{i,j}i + \sum_{i=0}^{p_j}a_{i,j} (-i+1) \right)$$ $$ m \alpha = \sum_{j=0}^m (\beta_j + \gamma_j) n_j$$ Où nous avons posé : $$\gamma_j = \frac{1}{n_j} \sum_{i=0}^{p_j} a_{i,j} (-i+1)$$

Cette dernière équation est ce que nous appellerons "l'équation additive des HM-graphe" : $$ \alpha = \frac{1}{m} \sum_{j=0}^m (\beta_j + \gamma_j) n_j$$

2.2 L'équation multiplicative des HM-graphes

En revenant aux formules initiales nous avons également : $$\alpha^m = \prod_{j=1}^m \sum_{i=0}^{p_j} a_{i,j}$$ $$\alpha^m = \prod_{j=1}^m \sum_{i=0}^{p_j} a_{i,j} (i - i + 1)$$ $$\alpha^m = \prod_{j=1}^m \left( \sum_{i=0}^{p_j} a_{i,j} i + \sum_{i=0}^{p_j} a_{i,j} (- i + 1) \right)$$ $$\alpha^m = \prod_{j=1}^m (\beta_j + \gamma_j) n_j$$ $$\alpha = \sqrt[m]{\zeta} \prod_{j=1}^m \sqrt[m]{\beta_j + \gamma_j} $$ Où nous avons posé \(\zeta = \prod_{j=1}^m n_j\), une constante du problème. C'est cette dernière équation que nous nommons "équation multiplicative des HM-graphes".

2.3 L'équation alternative additive des HM-graphes

Nous avons vu que l'établissement d'une relation entre \(\alpha\) et les \(\beta_j\) a nécessité l'introduction d'un nouveau paramètre : \(\gamma_j = \frac{1}{n_j} \sum_{i=0}^{p_j} a_{i,j} (-i+1)\). Nous allons tenter ici, une réécriture de l'équation de base en modifiant ce nouveau paramètre \(\gamma_j \).

Posons le changement d'indice \(k = i - p_j\), nous avons alors : $$\gamma_j = \frac{1}{n_j} \sum_{k = -p_j}^0 a_{p_j + k,j} (-p_j -k+1)$$ $$\gamma_j = \frac{1}{n_j} \left( -p_j \sum_{k = -p_j}^0 a_{p_j + k,j} - \sum_{k = -p_j}^0 a_{p_j + k,j} k + \sum_{k = -p_j}^0 a_{p_j + k,j} \right)$$ Bien sûr, nous avons : $$ \sum_{k = -p_j}^0 a_{p_j + k,j} = \alpha $$ Donc nous avons : $$ \gamma_j = \frac{1}{n_j} (-p_j + 1) \alpha - \delta_j$$ Où nous avons définit \(\delta_j = \frac{1}{n_j} \sum_{k = -p_j}^0 a_{p_j + k,j} k \) le paramètre alternatif. Ainsi en remplaçant dans l'équation additive on a alors : $$\alpha = \frac{1}{m} \sum_{j=1}^m \left( \beta_j + \frac{1}{n_j} (-p_j + 1) \alpha - \delta_j \right) n_j $$ $$ m \alpha = \sum_{j=1}^m (\beta_j - \delta_j ) n_j - \alpha \sum_{j=1}^m p_j + m \alpha$$ D'où l'équation alternative additive des HM-graphes : $$ \alpha = \frac{1}{\tau} \sum_{j=1}^m (\beta_j - \delta_j ) n_j $$ Où nous avons posé \( \tau = \sum_{j=1}^m p_j\), une constante dans le problème.

2.4 L'équation alternative multiplicative des HM-graphes

Tout d'abord nous avons : $$(\beta_j - \delta_j ) n_j = \sum_{i=0}^{p_j} a_{i,j} i + \sum_{i = -p_j}^0 a_{p_j + i,j} i = p_j \alpha$$ D'où : $$ \epsilon \alpha^m = \prod_{j=1}^m (\beta_j - \delta_j ) n_j $$ Avec \( \epsilon = \prod_{j=1}^m p_j \) , d'où l'équation multiplicative alternative des HM-graphes : $$ \alpha = \sqrt[m]{\frac{\zeta}{\epsilon}} \prod_{j=1}^m \sqrt[m]{\beta_j - \delta_j } $$

3- Applications à certains graphes

Dans toute cette partie nous allons voir comment appliquer l'équation générale qu'on a trouvé à différents graphes particuliers. Comme nous l'avons vu, nous allons devoir exprimer les termes \(\gamma_j \) pour réellement trouver l'équation du graphe.

3.1 Graphe linéaire

Un graphe linéaire est l'une des formes les plus simples de graphes :

Ici, il n'y a qu'un seul type d'arêtes, ce nombre d'arêtes sera noté \(\beta\) pour plus de lisibilité. Même si ici, il est évident que \( \alpha = \beta + 1 \), il est intéressant de voir comment l'équation générale nous permet de retrouver ce résultat.

Du fait des types d'arêtes, l'équation initiale se réduit désormais à : $$ \alpha = 2( \beta + \gamma) $$ Explicitons \( \gamma \): $$ \alpha = 2 \beta + ( a_0 - a_2)$$ \(a_0\) est le nombre de points ayant \(0\) arête, ici, il n'y a aucun point isolé donc \(a_0 = 0\). Et \(a_2\) est le nombre de points ayant \(2\) arêtes. Donc sauf les extrémités de la ligne, tous les autres points ont effectivement \(2\) arêtes donc \(a_2 = \alpha - 2\). Nous obtenons alors : $$\alpha = 2 \beta - (\alpha - 2)$$ $$2 \alpha = 2 \beta + 2$$ $$\alpha = \beta + 1$$ Voici un exemple simple de comment nous procéderons par la suite pour établir l'équation de n'importe quel graphe.

3.2 Pavage carré

Maintenant, étudions un graphe un peu plus complexe, le graphe "carré", ou pavage carré du plan. Bien sûr le graphe est fini. Et comme pour n'importe quel carré, le nombre total de ses points égal au carré du nombre de points sur un seul des côtés du carré. Ainsi il y a \( \sqrt{\alpha}\) sur un seul de ses côtés. Voici une représentation du graphe carré à 16 points (4 points sur une arrête) :

Reprenons notre équation initiale. Il s'agit toujours d'un graphe simple (pas d'hypergraphe). Et donc l'équation s'écrit : $$ \alpha = 2 \beta + 2 \gamma$$ Ici, le nombre maximal que peut supporter un point est \(4\) si bien que \(p = 4\), nous avons : $$\alpha = 2 \beta + \sum_{i = 0}^4 a_i (-i+1)$$ $$\alpha = 2 \beta + a_0 - a_2 - 2a_3 - 3a_4$$ Ici, bien sûr, il n'y a toujours pas de points isolés, donc \(a_0 = 0\). Seuls les \(4\) points extrêmes de chaque arête possèdent \(2\) arêtes, donc \(a_2 = 4\). Les points ayant \(3\) arêtes se situent sur les \(4\) arêtes du graphe carré, sauf les extrêmités. Chaque arêtes comptant \(\sqrt{\alpha}\) points, on a : \(a_3 = 4 (\sqrt{\alpha} -2 )\). Et le nombre de points ayant \(4\) arêtes sont les nombres de points restants, on a donc : \(a_4 = \alpha - a_2 - a_3\). D'où : $$ \alpha = 2 \beta - a_2 - 2 a_3 - 3 (\alpha - a_2 - a_3 ) $$ $$ 4 \alpha = 2 \beta - a_2 - 2 a_3 + 3a_2 + 3 a_3 $$ $$ 4 \alpha = 2 \beta + 2a_2 + a_3 $$ $$ 4 \alpha = 2 \beta + 4 \sqrt{\alpha} $$ $$ \alpha = \frac{\beta}{2} + \sqrt{\alpha}$$ On peut transformer un peu l'équation obtenue par passage au carré : $$ \alpha^2 - \alpha (1+ \beta )+ \frac{\beta^2}{4} = 0$$

3.3 Graphe complet

Considérons un graphe complet, c'est-à-dire un graphe dont un point est relié à tous les autres. Il s'agit d'un graphe classique, donc nous avons toujours l'équation qui s'écrit sous cette forme : $$\alpha = 2 \beta + 2 \gamma$$ Ici, tous les points sont reliés à tous les autres sauf eux-mêmes. Donc tous les points ont \( \alpha - 1\) arêtes. Ainsi pour tout \(i\), \(a_i = 0\) sauf pour \(i = \alpha - 1\) où là nous avons : \(a_{\alpha - 1} = \alpha\). D'où : $$\alpha = 2 \beta - (\alpha - 2)a_{\alpha - 1}$$ $$\alpha = 2 \beta - (\alpha - 2) \alpha$$ $$\alpha^2 - \alpha = 2 \beta$$ $$ \beta = \frac{\alpha(\alpha - 1)}{2}$$ Qui est l'équation d'un graphe complet.

3.4 Hypgergraphe complet

Nous élargissons ici la notion de graphe complet à celui d'hypergraphe complet. Un hypergraphe complet, est un hypergraphe ayant \(m\) types d'arêtes et où chaque point est relié une seule fois, à tous les autres points. Pour ce dernier exemple, il est bien plus naturel de raisonner différemment.

Tout d'abord, commençons, par numéroter les points de \(1\) à \(\alpha\). Et notons \(b_{i,j}\) le nombre d'arêtes de type \(j\) attachées au point numéro \(i\). Puisque qu'une arête de type \(j\) est commune à \(n_j\) points et que par définition, chaque point est relié à tous les autres une seule fois. Il faut que pour chaque point numéro \(i\) allant de \(1\) à \(\alpha\): $$\sum_{j=1}^m (n_j - 1) b_{i,j} = \alpha - 1$$ D'où : $$ \sum_{i=1}^{\alpha} \sum_{j=1}^m (n_j - 1) b_{i,j} = \alpha (\alpha - 1)$$ Dans cette formalisation, nous avons que : $$\beta_j = \frac{1}{n_j} \sum_{i=1}^{\alpha} b_{i,j}$$ On peut alors réécrire en intervertissant les sommes: $$ \sum_{j=1}^m \sum_{i=1}^{\alpha} (n_j - 1) b_{i,j} = \alpha (\alpha - 1)$$ $$ \sum_{j=1}^m (n_j - 1) \sum_{i=1}^{\alpha} b_{i,j} = \alpha (\alpha - 1)$$ $$ \sum_{j=1}^m n_j(n_j - 1) \beta_j = \alpha (\alpha - 1)$$ Ecrit plus joliment nous obtenons l'équation de l'hypergraphe complet : $$ \sum_{j=1}^m \binom{n_j}{2} \beta_j = \binom{\alpha}{2}$$