1- Introduction

Le nombre d'or est un nombre connu depuis des siècles. Il est l'unique solution positive de l'équation du second degré \(x^2 - x - 1 = 0 \). On le note souvent \(\phi\) et son expression quadratique est \(\varphi = \frac{1 + \sqrt{5}}{2}\). Ce nombre a des propriétés très intéressantes notamment géométrique. Il est associé à la spirale d'or, qui a pour allure :

2- Propriétés élémentaires du nombre d'or

2.1 Une autre expression du nombre d'or

On a une autre écriture du nombre d'or : $$\varphi = \sqrt{\frac{5 + \sqrt{5}}{5 -\sqrt{5}}} $$

Démonstration

On passe au carré : $$ \left( \sqrt{ \frac{5 + \sqrt{5}}{5 - \sqrt{5}} }\right)^2 = \frac{25}{20} + \frac{10 \sqrt{5}}{20} + \frac{5}{20} = \frac{3}{2} + \frac{\sqrt{5}}{2} $$ D'autre part : $$ \left( \frac{1 + \sqrt{5}}{2}\right)^2 = \frac{3}{2} + \frac{\sqrt{5}}{2} $$ D'où l'égalité en prenant la racine carré (il s'agit bien de deux nombres positifs).

2.2 Factorisations et identités du nombre d'or

En remarquant que le nombre d'or est solution de l'équation \( x^2 - x - 1 = 0 \) on peut décrire plusieurs petites propriétés algébriques du nombre d'or. Une factorisation du nombre d'or : $$ \varphi = (\varphi - 1)(\varphi + 1)$$ Une factorisation de \( 1\): $$ 1 = (\varphi - \sqrt{\varphi})(\varphi + \sqrt{\varphi}) $$ La relation carré-inverse: $$\varphi^2 - \frac{1}{\varphi} = 2$$

2.3 Puissances du nombre d'or

$$\forall n \ge 2, \varphi^n = \varphi^{n-1} + \varphi^{n-2}$$

Démonstration

On peut procéder par récurrence sur \(n\): Pour \(n = 2\) on a bien \(\varphi^2 = \varphi + 1\). Et supposons que pour un \(n\) quelconque plus grand que 2, l'identité soit vraie, dans ce cas : $$\varphi^{n+1} = \varphi \varphi^{n} = \varphi ( \varphi^{n-1} + \varphi^{n-2}) = \varphi^{n} + \varphi^{n-1}$$

3- Théorie des nombres métalliques

3.1 Définition et existence de la suite des nombres métalliques

On se donne l'équation suivante pour \(n \in \mathbb{N}^*\) : $$x^n = \sum_{k = 0}^{n-1} x^k$$ Pour chaque \(n \in \mathbb{N}^*\) , cette équation a une unique solution positive.
Pour \(n = 1\) on a $$x = 1$$ Pour \(n = 2\) on a $$x^2 - x - 1 = 0$$ dont l'unique solution positive est le nombre d'or \( \varphi \).
Pour \(n = 3\) on a $$x^3 - x^2 - x - 1 = 0$$ dont l'unique solution postive est le nombre dit "d'argent" qu'on peut noter \(\varphi_{2}\): $$ \varphi_{2} = \frac{1}{3} \left( 1 + - \sqrt[3]{19-3 \sqrt{33}} + \sqrt[3]{19 + 3\sqrt{33}} \right) $$

Démonstration

On pose la fonction polynômiale \( \Psi_p\) suivante (dépendante de l'entier \( p \)): $$\forall x \in \mathbb{R} , \Psi_p(x) = x^p - \sum_{k=0}^{p-1} $$

Où on a représenté \(\Psi_2\) en bleu, \(\Psi_3\) en rouge, \(\Psi_4\) en vert et \(\Psi_5\) en gris. On voit bien que les solutions positives (la suite des nombres métalliques) croit et elle semble converger vers \(2\), c'est ce qu'on va montrer plus tard.

Existence de la racine positive

On va utiliser le théorème des valeurs intermédiaires sur la fonction \(\Psi_p\) et sur l'intervalle \( [1,3] \). On calcule alors \(\Psi_p (1)\) et \(\Psi_p (3)\) : $$\Psi_p (1) = 1 - \sum_{k = 0}^{p-1} 1 = 1 - p < 0$$ car \(p > 1\) (et égal à \(0\) si \( p = 1 \) mais on a déjà prouvé l'existence de la racine positive pour \(\Psi_1 \) plus haut).

Pour \( x= 3\) : $$\Psi_p (3) = 3^p - \sum_{k=0}^{p-1} 3^k = 3^p - \frac{1}{2} (3^p - 1) = \frac{3^p}{2} + \frac{1}{2} > 0$$ Et puisque les \(\Psi_p\) sont continues sur cet intervalle (même sur \(\mathbb{R})\)) en tant que fonctions polynômiales alors le théorème des valeurs intermédiaires nous assure de l'existence d'une racine dans l'intervalle \([1,3]\) (et donc bien une racine positive).

Unicité de la racine positive

On cherche alors à simplifier l'expression de \(\Psi_p (x)\). Si \(x \neq 1\) alors $$\Psi_p(x) = x^p - \frac{x^p -1}{x - 1}$$ et sinon $$\Psi_p(x) = 1 - p$$ Pour \(2 \le p\) , \(1\) n'est pas racine de \(\Psi_p\), on se concentre alors sur la première expression de \(\Psi_p(x)\) : $$\Psi_p(x) = x^p - \frac{x^p -1}{x - 1} = \frac{x^{p+1} - 2x^p +1}{x-1}$$ qui est nulle si et seulement si: $$ C_p(x) = x^{p+1} - 2x^p + 1 = 0$$ \(C_p\) est dérivable et : $$ \forall x \in \mathbb{R}, C_p'(x) = (p+1)x^p - 2px^{p-1} = x^{p-1}((p+1)x - 2p)$$ D'où: $$C_p'(x) = 0 \Leftrightarrow x^{p-1}((p+1)x - 2p) = 0 $$ Donc les racines de \(C_p'\) sont \( 0\) et \( \frac{2p}{p+1}\). On voit aussi que le signe de \(C_p'\) va dépendre de la parité de \(p\) mais sur l'intervalle \( ]0, + \infty [ \), on a le même tableau de variation. Voici par exemple le tableau de variation de \(C_p\) pour \(p\) pair :

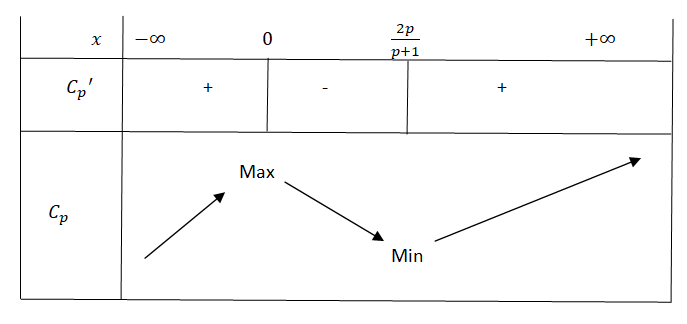
On constate donc que la fonction \(C_p\) admet un minimum sur \( ]0, + \infty[ \) qui est atteint en \(\frac{2p}{p+1}\) qui est négatif, tout comme en \(0\) où la fonction vaut \(-1\). Donc elle est négative sur \([0, \frac{2p}{p+1}] \). De plus elle tend vers \( + \infty\) en \(+ \infty \) (elle est aussi strictement croissante). D'où le fait qu'elle ne s'annule bien qu'une seule fois sur l'intervalle \( [\frac{2p}{p+1}, + \infty[ \).

3.2 Croissance de la suite des nombres métalliques

On reprend la fonction \(C_p\) : $$\forall x \in \mathbb{R}, C_p(x) = x^{p+1} - 2x^p + 1$$ Et pour rappel : $$ C_p (\varphi_p) = \varphi_p^{p+1} - 2 \varphi_p^{p} + 1 = 0 \Leftrightarrow \varphi_p^{p} (2 - \varphi_p) = 1$$ Et comme \(\varphi_p \neq 0 \): $$\varphi_{p+1}^{p+1} (2 - \varphi_{p+1}) = 1 \Leftrightarrow \varphi_{p+1}^{p} (2 - \varphi_{p+1}) = \frac{1}{\varphi_{p+1}}$$ De plus, on a que : $$C_p (\varphi_{p+1}) = \varphi_{p+1}^p (\varphi_{p+1}-2) + 1 \Leftrightarrow C_p (\varphi_{p+1}) = 1 - \frac{1}{\varphi_{p+1}}$$ Et on a donc : $$C_p(\varphi_{p+1}) = 1 - \frac{1}{\varphi_{p+1}} > 0$$ Par stricte croissance de \(C_p\), on peut conclure que : $$C_p(\varphi_{p+1}) > C_p(\varphi_p) = 0 \Leftrightarrow \varphi_{p+1} > \varphi_p$$ Donc la suite des nombres métalliques est strictement croissante.

3.3 Convergence de la suite des nombres métalliques

On utilise le théorème des valeurs intermédiaires sur la fonction \(\Psi_p\) entre \(\frac{2p}{p+1}\) et \(2\), qui nous assure que les nombres métalliques sont compris dans cet intervalle. Donc la suite est bornée (par \(2\)). D'après le théorème de la limite monotone, elle converge vers une limite \(l\) inférieure ou égale à \(2\). Et comme lorsque \(p \rightarrow + \infty \) alors \(\frac{2p}{p+1} \rightarrow 2\) d'où : $$\lim_{n \to \infty} \varphi_n = 2$$

4- Suites convergeant vers le nombre d'or

4.1 Développement du nombre d'or en fractions continues

Le nombre d'or vérifie l'équation \( \varphi = 1 + \frac{1}{\varphi}\). On peut donc écrire par des remplacement successifs que \(\varphi = 1 + \frac{1}{1 + \frac{1}{\varphi}}\) procédé qu'on peut répéter à l'infini. Ainsi il semblerait que le nombre d'or vérifie \(\varphi = 1 + \frac{1}{1 + \frac{1}{ 1 + \frac{1}{1 + \frac{1}{1 +...}}}}\). On va le démontrer rigoureusement en utilisant la suite $$ \begin{cases} v_0 = 1 \\ v_{n+1} = 1 + \frac{1}{v_n} \end{cases} $$. On démontre qu'elle est convergente puis que sa limite est le nombre d'or.

Démonstration

On sépare la suite \((v_n)_{n \in \mathbb{N}}\) en deux sous-suites \((a_n)_{n \in \mathbb{N}}\) qui est la sous-suite des terme pairs de \((v_n)_{n \in \mathbb{N}}\) et \((b_n)_{n \in \mathbb{N}}\) qui est la sous-suite des terme impairs de \((v_n)_{n \in \mathbb{N}}\).

Etude d'une fonction

Soit \( G \) la fonction suivante : $$ \forall x \in [1,2], G(x) = 1 + \frac{1}{x} $$ et qui a pour dérivée : $$\forall x \in [1,2], G'(x) = - \frac{1}{x^2} < 0 $$ Donc \(G \) est strictement décroissante sur \([1,2]\). De plus, \(G\) est minorée par \(G(2) = \frac{3}{2}\) et majorée par \(G(1) = 2\).

Croissance et majoration de \((a_n)_{n \in \mathbb{N}}\)

On a : $$\forall n \in \mathbb{N}, a_{n+1} = v_{2n+2} = 1 + \frac{1}{v_{2n+1}} = 1 + \frac{1}{1 + \frac{1}{v_{2n}}} = 1 + \frac{v_{2n}}{v_{2n} + 1} = 1 + \frac{a_n}{a_n + 1}$$ De plus il est clair que \((a_n)_{n \in \mathbb{N}}\) est une suite à valeurs dans \([1,2]\) (récurrence immédiate). Procédons par récurrence pour montrer que \((a_n)_{n \in \mathbb{N}}\) est croissante. Pour l'initialisation, elle est claire : $$a_1 > 1 = a_0$$ Pour l'hérédité, on suppose que $$a_{n+1} > a_n$$ D'où en appliquant \(G\) strictement décroissante : $$G(a_{n+1}) < G(a_n) $$ $$G(G(a_{n+1})) > G(G(a_n))$$ D'où : $$a_{n+2} > a_{n+1}$$ Pour la majoration, on procède également par récurrence, on montera que la suite est majorée par \(2\). L'initialisation est encore évidente. Pour l'hérédité, on part de $$2 > a_n$$ $$G(2) < G(a_n)$$ $$G \left(\frac{3}{2} \right) > G(G(a_n))$$ $$ 2 > 1 + \frac{2}{3} > a_{n+1}$$ D'où la conclusion que la suite \((a_n)_{n \in \mathbb{N}}\) est strictement croissante et majorée par \(2\). Donc elle converge vers une limite inférieure ou égale à \(2\).

Décroissance et minoration de \((b_n)_{n \in \mathbb{N}}\)

On a, de même : $$b_{n+1} = 1 + \frac{b_n}{b_n + 1}$$ De plus \((b_n)_{n \in \mathbb{N}}\) prend bien ses valeurs dans \([1,2]\). On montre alors que \((b_n)_{n \in \mathbb{N}}\) est strictement décroissante à partir du rang \(1\), par réccurence. Pour l'initialisation c'est clair : $$b_1 = v_3 = \frac{5}{3} > 1 + \frac{3}{5} = \frac{8}{5} = b_2$$ Pour l'hérédité, on suppose que : $$b_{n+1} < b_n $$ $$G(b_{n+1}) > G(b_n)$$ $$G(G(b_{n+1})) < G(G(b_n))$$ $$b_{n+2} < b_{n+1}$$ Pour la minoration, on procède également par récurrence, et on montre que la suite \((b_n)_{n \in \mathbb{N}}\) est minorée par \(1\). Pour l'initialisation c'est évident : $$b_0 = v_1 = \frac{3}{2} > 1$$ Pour l'hérédité, on suppose que $$b_n > 1$$ Dans ce cas : $$G(b_n) < G(1)$$ $$G(G(b_n)) > G(G(1))$$ $$b_{n+1} > \frac{3}{2} > 1$$ D'où \((b_n)_{n \in \mathbb{N}}\) est strictement décroissante et minorée, donc elle converge vers une limite supérieure ou égale à \(1\) d'après le théorème de la limite monotone.

Convergence et limite

Puisque \((a_n)_{n \in \mathbb{N}}\) et \((b_n)_{n \in \mathbb{N}}\) convergent et ont la même équation de récurrence et sont toutes les deux des suites positives (donc leur limite est positive) alors elles convergent vers la même limite qui vérifient : $$L = 1 + \frac{L}{1 + L}$$ $$L^2 - L - 1 = 0$$ D'où $$L = \varphi$$ puisque la limite doit être positive. Puisque les deux sous-suites paires et impaires de \((v_n)_{n \in \mathbb{N}}\) convergent vers la même limite alors \((v_n)_{n \in \mathbb{N}}\) converge également vers \(\varphi\).

4.2 Développement du nombre d'or en racines imbriquées

De même, le nombre d'or vérifie l'équation \( \varphi = \sqrt{1 + \varphi}\). On peut donc écrire par des remplacement successifs que \( \varphi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + ...}}}}}\) procédé qu'on peut répéter à l'infini. C'est ce qu'on appelle un "développement en racines imbriquées du nombre d'or". On va le démontrer rigoureusement en utilisant la suite $$ \begin{cases} u_0 = 1 \\ u_{n+1} = \sqrt{1+u_n} \end{cases} $$. On démontre qu'elle est convergente puis que sa limite est le nombre d'or.

Démonstration

Tout d'abord, la suite \((u_n)_{n \in \mathbb{N}}\) est positive (par récurrence immédiate). De plus, elle est croissante, on peut le démontrer par récurrence. L'initialisation est immédiate : \(u_1 = \sqrt{2} > u_0 = 1\). Pour l'hérédité, on part de l'hypothèse de récurrence : $$u_{n+1} > u_n$$ $$1 + u_{n+1} > 1 + u_n $$ $$u_{n+2} > u_{n+1}$$ Car la racine carrée est croissante et que la suite \((u_n)_{n \in \mathbb{N}}\) est positive. De plus, cette suite est majorée par le nombre d'or. On le montre par récurrence. Pour l'initialisation, c'est immédiat : \(u_0 = 1 < \varphi\). Pour l'hérédité, on suppose par hypothèse que : $$u_n < \varphi$$ $$u_n + 1 < \varphi + 1$$ $$\sqrt{u_n + 1} < \sqrt{1 + \varphi}$$ $$u_{n+1} < \varphi$$ Donc la suite est croissante et majorée et elle converge vers une limite positive qui vérifie (par passage à la limite dans l'équation de récurrence): $$L = \sqrt{1 + L}$$ $$L^2 - L - 1 = 0$$ D'où : $$ L = \varphi$$

5- Théorie des nombres auxiliaires

5.1 Définition et propriétés des nombres auxiliaires

Les nombres auxiliaires sont définis comme étant les uniques solutions positives des solutions du second degré suivantes : \(x^2 - px - 1 = 0\) avec \(p\) un nombre entier strictement positif. Ainsi le nombre d'or est le premier nombre auxiliaire, puisque c'est la solution positive à l'équation auxiliaire pour \(p = 1\). Si on résout cette équation du second degré, on peut directement exprimer les nombres auxiliaires en fonction de l'entier \(p\), on les notera alors \( \beta_p\): $$\beta_p = \frac{p + \sqrt{p^2+4}}{2}$$ Le nombre dit "d'argent" s'écrirait alors \(\beta_2 = 1 + \sqrt{2} \).

5.2 Développement des nombres auxiliaires en fractions continues et en racines imbriquées

D'après la relation vérifiée par \(\beta_p\), on peut en déduire le développement de \(\beta_p\) en fractions continues et en racines imbriquées : $$\beta_p = p + \frac{1}{p + \frac{1}{ p + \frac{1}{p + \frac{1}{p +...}}}} = \sqrt{p + \sqrt{p + \sqrt{p + \sqrt{p + \sqrt{p + ...}}}}} $$ (Démonstrations similaires que pour le nombre d'or). On comprend ainsi pourquoi ces nombres généralisent le nombre d'or, puisqu'ils généralisent ses propriétés.

5.3 Puissances du nombre des nombres auxiliaires et polynômes de Fibonacci

Les polynômes de Fibonacci sont une famille de polynômes définis par une relation de réccurence précise : $$ F_0(x) = 0 $$ $$ F_1(x) = 1 $$ $$ F_{n}(x) = x F_{n-1}(x) + F_{n-2}(x) $$ La dernière égalité étant valable pour \(n \ge 2\). On va prouver que : $$ \forall n \in \mathbb{N}^{*}, \beta_{p}^n = F_{n}(p) \beta_{p} + F_{n-1}(p)$$

Démonstration

Pour cela on effectue une démonstration par réccurence sur \(n\).

Pour \(n = 1\), on a : \( \beta_{p}^1 = F_{1}(p) \beta_{p} + F_{0}(p) \) ce qui est vrai d'après la définition de la suite des polynômes de Fibonacci. Pour l'hérédité, on suppose que la propriété est vraie à un rang \(n\) quelconque plus grand que 2, dans ce cas, on a : $$\beta_p^{n+1} = \beta_p \beta_p^{n} $$ $$\beta_p^{n+1} = \beta_p (F_{n}(p) \beta_{p} + F_{n-1}(p))$$ $$\beta_p^{n+1} = F_{n}(p) \beta_{p}^2 + \beta_{p} F_{n-1}(p))$$ $$\beta_p^{n+1} = F_{n}(p) (p \beta_p + 1) + \beta_{p} F_{n-1}(p))$$ $$\beta_p^{n+1} = (F_{n}(p) p + F_{n-1}(p) )\beta_p + F_{n}(p) $$ $$\beta_p^{n+1} = F_{n+1}(p) \beta_p + F_{n}(p) $$ Ce qui prouve l'hérédité et conclut la récurrence. Pour information, pour \(p = 1\), les polynômes correspondant sont en réalité les nombres de Fibonacci. Ainsi pour le nombre d'or, on a en particulier : $$ \phi^{n} = F_{n} \phi + F_{n-1} $$ Pour \(n \ge 2\).

6- Une autre généralisation du nombre d'or

6.1 Nombre métalliques alternatifs

Le nombre de plastique est l'unique solution positive de l'équation $$x^3 = x + 1$$ Noté \(\psi\) il vaut : $$\psi = \sqrt[3]{\frac{1}{2} + \frac{\sqrt{69}}{18}} + \sqrt[3]{\frac{1}{2} - \frac{\sqrt{69}}{18}}$$ Chaque équation de la forme $$x^n = x + 1$$ possède une unique solution réelle positive pour \(n \ge 2\), et on appelle cette suite de solution positive les "nombres métalliques alternatifs", qu'on notera \(\psi_n\).

Démonstration

On va démontrer qu'il existe une unique solution réelle positive à chacune des équation \( x^n = x + 1\) avec \(n \ge 2\) : Posons la fonction $$f(x) = x^n - x - 1$$, elle est évidemment dérivable sur \(\mathbb{R}\) en tant que polynôme sa dérivée vaut : $$f'(x) = n x^{n-1} - 1$$ On a alors : $$f'(x) = 0 \iff x^{n-1} = \frac{1}{n} $$

Cas \(n\) pair

Equation qui possède une unique solution si \(n-1\) est impair et donc \(n\) pair puisque tout polynôme de degré impair est bijectif sur \(\mathbb{R}\) (injectif et surjectif). Cette unique solution est donc dans le cas \(n\) pair : $$x = \frac{1}{\sqrt[n-1]{n}}$$ On peut donc dire en étudiant le signe de sa dérivée, que \(f \) est strictement croissante sur l'intervalle \(]\frac{1}{\sqrt[n-1]{n}}, \infty[ \)et strictement décroissante sur \(]-\infty, \frac{1}{\sqrt[n-1]{n}}[ \). Elle admet donc un minimum global en \( \frac{1}{\sqrt[n-1]{n}} \) qui est évidemment négatif : \( f \left( \frac{1}{\sqrt[n-1]{n}} \right) = \frac{1}{n^{\frac{n}{n-1}}} - \frac{1}{n^{\frac{1}{n-1}}} - 1 \) avec \( \frac{1}{n^{\frac{n}{n-1}}} < 1 \) ce qui prouve que le minimum est strictement négatif. Donc \(f\) est strictement croissante sur \( ]\frac{1}{\sqrt[n-1]{n}}, +\infty[\) et comme elle est continue, d'après le théorème de la bijection, il existe un unique solution à l'équation \(f(x) = 0\) sur l'intervalle \( ]\frac{1}{\sqrt[n-1]{n}}, +\infty[\). De plus, on a \(f(0) = - 1 \) donc \(f\) est également strictement négative sur \( [0, \frac{1}{\sqrt[n-1]{n}}[\) (puisqu'elle est strictement décroissante sur cet intervalle \( -1\) est un majorant de \(f\) sur cet intervalle). Donc \(f\) admet bien une unique solution positive.

Cas \(n\) impair

Dans ce cas, la dérivée de \(f\) est un polynôme pair : $$f'(x) = nx^{n-1} - 1$$ On se place sur \(\mathbb{R}^+\). Sur cet intervalle, \(f'(x) = 0 \iff x = \sqrt[n]{\frac{1}{n}} \) puisque la racine \(n\) -ième d'un nombre positif est précisément l'unique solution positive de l'équation \(x^n = a \) avec \(a\) un réel positif. Et de même que pour le cas précédent, \(f\) est strictement croissante sur \(]\frac{1}{\sqrt[n-1]{n}}, \infty[ \) et strictement décroissante sur \( [0, \frac{1}{\sqrt[n-1]{n}}[\) où elle est majorée par \(1\). Elle admet donc bien elle aussi, une unique solution positive.

6.2 Développements en racines imbriquées

On va démontrer que pour tout \(n \in \mathbb{N} \) à l'exception de \(n = 0\) ou \(n = 1\) on a : $$\psi_n = \sqrt[n]{1 + \sqrt[n]{1 + \sqrt[n]{1 + ...}}}$$

Démonstration

On pose pour cela la suite \((g_n)_{n \in \mathbb{N}}\) définie par : $$ \begin{cases} g_0 = 1 \\ g_{n+1} = \sqrt[m]{1 + g_n} & \text{si }n\text{ est plus grand que }1 \end{cases}$$ Cette suite est bien définie puisque chaque terme de la suite est bien positif (récurrence immédiate). De plus cette suite est strictement croissante (démonstration par récurrence similaire à celle pour le développement imbriquée du nombre d'or). De plus cette suite est également majorée par \(\psi_m\) par récurrence (démonstration également similaire). On peut donc conclure que \((g_n)_{n \in \mathbb{N}}\) converge d'après le théorème de la limite monotone, vers une limite \(L\) inférieure ou égale à \(\psi_m\) puis en passant à la limite dans l'égalité de récurrence, on obtient que \(L\) vérifie que : \(L = \sqrt[m]{1 + L}\) d'où \(L = \psi_m\).